Written By Juan David Delgado
FILTRO FIR (FILTRO DE RESPUESTA FINITA AL IMPULSO)
Son conocidos como filtros digitales no recursivos debido a que no poseen la retroalimentación que es la parte recursiva de un filtro. Pueden ser diseñados usando diferentes métodos, pero la mayoría de ellos esta diseñado a la aproximación del filtro ideal. El objetivo no es lograr un filtro idea, ya que es casi imposible, la idea es lograr la mayor cantidad de características buenas posibles. La función de transferencia del filtro FIR se aproxima al ideal a medida de que el orden del filtro aumenta, pero asi mismo aumenta la complejidad y la cantidad de tiempo necesaria para procesar las muestras de entrada de la señal que es filtrada.
El resultado de respuesta en frecuencia puede ser una función monótona o una función osciladora con cierto rango de frecuencia. La forma de onda de la respuesta en frecuencia depende del método usado en el proceso de diseño así como también de los parámetros usados.
Existen varios métodos usados para diseñar los filtros FIR, el mas comun es el metodo de la ventana porque es simple y eficiente, el metodo de muestreo de frecuencia es facil de usar, pero tiene una atenuación baja el la banda de detención.
DISEÑO
Para poder diseñar este tipo de filtro primero se deben tener claros ciertos conceptos.
Tipos de Filtro
- Filtro Pasa Bajo (Low-Pass Filter): Este tipo de filtro se caracteriza por permitir el paso de las frecuencias más bajas y atenuar las frecuencias más altas.
- Filtro Pasa Alto (High-Pass Filter): Este tipo de filtro se caracteriza porque en su respuesta en frecuencia se atenúan las componentes de baja frecuencia y permite el paso en alta frecuencia.
- Filtro Pasa Banda (Band-Pass Filter): Este filtro se caracteriza por dejar pasar un determinado rango de frecuencias de una señal y atenúa el paso del resto.
- Filtro Rechaza Banda (Band-Stop Filter): Este filtro no permite el paso de señales cuyas frecuencias se encuentran comprendidas entre las frecuencias de corte superior e inferior.
Dependiendo del filtro se debe tener en cuenta dos posibilidades:
Tipos de Ventana
- Bartlett: Entrega un punto L en la ventana en la columna del vector w, L debe ser un entero positivo. Los coeficientes de la ventana se pueden calcular:

- Hann: Devuelve un punto L simetrico en la columna del vector w, L debe ser un entero positivo. Los coeficientes pueden ser calculados:

- Bartlett-Hanning: Esta ventana tiene un lóbulo principal en el origen y descomposición asintóticamente en los lóbulos laterales en ambos lados. Es una combinación lineal tabulada de las ventanas Bartlett y Hann con lóbulos laterales más bajos que Bartlett y Hann y con lóbulos laterales mucho más bajo que tanto Bartlett y ventanas de Hamming.

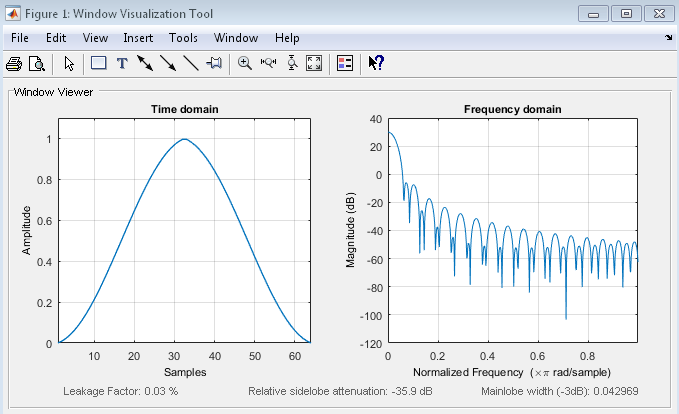
- Hamming: Los coeficientes de la ventana de Hamming se pueden calcular con la siguiente ecuación:


- Bohman: Es la convolución de la media duracion de dos lobulos cosenoidales. En el dominio del tiempo, es el producto de una ventana triangular y un ciclo sencillo de un coseno con un termino añadido para fijar la primera derivada a cero en el limite. Los coeficientes se pueden calcular:
- Blackman: Los coeficientes se pueden calcular:

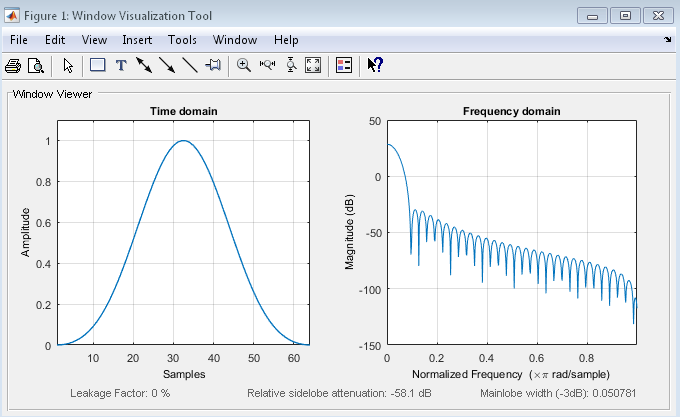
- Blackman-Harris: La ventana es mínima cuando los lóbulos laterales se hacen mínimos. Los coeficientes se pueden calcular:
Cuando es simétrico:
Cuando es periódico:
Una vez se tengan estos conceptos claros, se procede a diseñar el filtro en MATLAB.
- La primera parte del código consiste en asignar los parámetros que se usaran en el filtro. Entonces para empezar limpiamos todo lo que se tenia antes para evitar problemas, luego si se procede a asignar los parámetros.
- La segunda parte del codigo consiste en establecer que tipo de ventana y que tipo de filtro se usaran.
- La tercera parte es diseñar el filtro que usaremos, el funcionamiento que debe seguir el filtro se muestra en la siguiente imagen
La señal X[n] entra a un vector temporal Z, el cual ira multiplicandose con los coeficientes generados dependiendo del tipo de ventana y de filtro, y la señal de salida sera la sumatoria respectiva de la sumatoria de estas multiplicaciones. Este procedimiento se lleva a cabo en un ciclo, empezando desde que solo se llena una posición de cada vector hasta que todos los datos de la señal de entrada han entrado.
El código es el siguiente:
Los vectores "y" "h" "m" se inicializan todos en ceros.
Ejercicio:
Diseñe un filtro rechaza banda que elimine el ruido de la canción a una frecuencia de muestreo de 44100 Hz, el orden del filtro es 70. Use la ventana de Hamming.
Código:
En esta primera parte del código se declararon los parámetros que se usaran en el proceso de filtración del audio. Se declaro la frecuencia de corte mínima y la frecuencia de corte máxima que es la que permitirá filtrar el ruido existente entre esas frecuencias. Se estableció también el valor de la frecuencia de de muestre, también el valor de el orden del filtro, que recordando debe ser par.
En la linea 17 del código la ecuación del w(i) se usa la del tipo de ventana Hamming, en la linea 19 y 21 son las ecuaciones correspondientes al tipo de filtro que en este caso es un filtro rechaza banda. En la linea 23 se hace la multiplicación de la frecuencia del tipo de ventana con el valor correspondiente al filtro rechaza banda para generar los coeficientes del filtro.
En la linea 29 se establece que la señal de entrada "x" sera la lectura de un archivo de audio, el cual podrá encontrar en el archivo
Filtro.rar. ademas en la linea 32 se gráfica la señal entrante que se muestra en la imagen de la señal sin filtrar mas adelante.
En esta parte final se procede a filtrar la señal como se comento anteriormente y se gráfica la señal de salida "y" ya filtrada que se muestra en la imagen de a continuación.
Como se observa en la figura, el ruido que existía antes de ser filtrada la señal desapareció luego del filtro.
En el vídeo se puede escuchar la señal sin filtrar
Ahora se puede escuchar la señal filtrada
AQUI encontrara la canción sin filtrar y el código en MATLAB para que lo pruebe y experimente con otros tipos de ventan y filtros.
Referecences:
Downloads: