Es un algoritmo que determina los elementos de una matriz que deberían seleccionarse para que juntos formen una línea. Esto se aplica para la matriz de pixeles que forman una pantalla.
Consiste en una aproximación de puntos tal que al pasar una línea por ellos haya el menor error posible, funciona con suma de enteros, restas y corrimientos, las cuales son operaciones que no requieren de mucho procesamiento y funcionen en cualquier arquitectura. Tiene la desventaja de ir aumentando su error a medida que se aumenta su complejidad, pero por ser tan sencillo en términos generales es bastante utilizado.
La convención que utiliza para hacer el barrido es el siguiente:
El valor del pixel aumenta a la derecha y hacia abajo, siendo la primera coordenada el valor de la columna y la segunda el valor de la fila. Es importante saber esto, ya que así es posible determinar la línea que se dibujará en función de su pendiente.
Sabiendo la pendiente de la línea que se va a dibujar se obtienen los pixeles que se siguen dibujando para dar forma a la línea basado en la siguiente fórmula:
Al usar el algoritmo, el resultado sería algo como esto:
function line(x0, y0, x1, y1)
real deltax := x1 - x0
real deltay := y1 - y0
real error := -1.0
real deltaerr := abs(deltay / deltax) // Asumir deltax != 0
// Es importante tener en cuenta los decimales en la división
int y := y0
for x from x0 to x1-1
plot(x,y)
error := error + deltaerr
if error ≥ 0.0 then
y := y + 1
error := error - 1.0
Se puede ver que se describe la función line, que como es nuestro objetivo dibujaría una línea en la pantalla. Esta función incluye 4 argumentos, los cuales son dos pixeles de la pantalla, cada uno con sus coordenadas, la línea recta que une a estos dos pixeles sería la que se mostraría en pantalla.
Para calcular la pendiente de la recta se halla primero dos deltas, el delta horizontal y vertical, con la división de éstas se tiene:
Donde el término de la izquierda es deltaerr.
Con esto empezamos a recorrer los pixeles que conforman la línea. Se tiene para X que se recorre desde X0 hasta X1, de la misma manera para Y. Usando la relación matemática se encuentra cuál es el error para cada pixel dibujado, que como se puede ver incrementa a cada iteración, esto se corrige variando la coordenada en Y, con esto el error se recalcula.
El siguiente paso para entender el algoritmo es implementarlo en software, yo lo implementé en C, pero cualquier lenguaje es útil.
El código es el siguiente:
En la primera parte está la descripción de la función tal y como en el pseudocódigo, en la segunda parte la declaración de la matriz, etc, lo importante es el uso de la función que dibuja la línea, en la cual se colocaron las coordenadas de la línea que se quería dibujar.
Al compilarlo se graficó así en forma de texto para hacerlo más sencillo:
Se puede concluir que la línea se dibujó con un código muy sencillo, pero se hizo evidente la desventaja del error al inicio de la línea, en este caso sobretodo porque se tenía una matriz muy pequeña, pero es un buen ejemplo para entender mejor cómo funciona el algoritmo.
Ahora es momento de implementarlo en hardware, primero en papel definimos que entradas y salidas tendría el chip y que más requeriríamos para su construcción.
- Una señal de start para indicar que se debe ejecutar el módulo, esto porque las coordenadas (x0,y0) y (x1,y1) son válidas.
- Cuatro entradas de 11 bits con las coordenadas correspondientes
- Una señal de salida plot, la cual indica que las coordenadas ingresadas hacen parte de la línea
- Dos señales x y y que llevan la información que se irá dibujando en cada pixel
- Una señal llamada done, para indicar que el proceso se ha terminado
Si se hace un análisis de los tiempos con las señales propuestas se tienen los siguientes comportamientos:
Se puede ver claramente el comportamiento de las señales x y y, según las entradas de coordenadas y después de que ha sido activado el pulso start. De igual manera cómo están sincronizadas la señal plot con la señal start y done formando lo que serían 3 estados del proceso.
Descripción en Verilog
Este módulo se trabaja en el proyecto de la
primera parte del tutorial, por lo que con éste abierto creamos un nuevo archivo de tipo systemverilog.
Un archivo systemverilog es una combinación entre un lenguaje de descripción de hardware y un lenguaje de verificación de hardware, funciona de manera muy similar a verilog, con la misma sintaxis.
La descripción como la indica la bibliografía es la siguiente:
Simulación
Después de describir el
módulo, conviene simular que las señales de salida se comporten como las que vimos antes en la teoría.
Es importante revisar la
sección de simulación en esta página para realizar la simulación de manera exitosa.
Para llegar a este punto se seleccionan las señales que se quieren simular, en la imagen se muestran cuales nos ayudarán a llegar a una buena conclusión.
Se comprueba que el proceso empiece con un flanco de subida de la señal start.
Se analiza el comportamiento. Para las mismas coordenadas analizadas en un diagrama de tiempos al principio de este manual se continuó la simulación después de que start se llevó a bajo y la señal plot se puso en alto, funcionando el algoritmo. Se observa que
X cambia de manera líneal y que
Y depende de la señal de error.
Err toma los mismos valores que se predijeron en el diagrama de tiempos.
Módulos adicionales:
Un framebuffer es una porción de RAM que contiene un mapa de bits de manera que al ser leída se puede reconstruir un frame. Allí se almacenan los valores de color para cada pixel.
Es posible incluir un canal alpha para generar el efecto visto en la parte 1 de este manual.
Éste módulo, tiene entradas de posición que indican dónde se está posicionando en la pantalla y dos señales para habilitar el color y la escritura, en este caso la línea. A la salida se tienen las señales de sincronización vertical y horizontal.
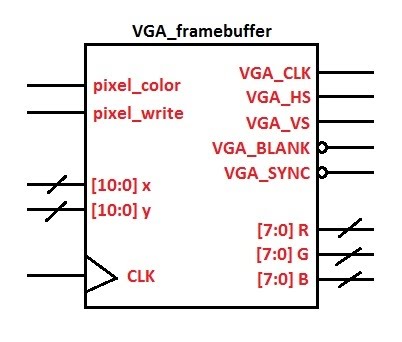
Para describir el módulo en verilog, después de indicar las entradas y salidas se indican algunos parámetros necesarios para las señales de sincronización a la salida, tal como se hizo con la primera parte.


Se usan dos contadores, uno horizontal y otro vertical para el barrido de la imagen, ambos a la velocidad del reloj de 50MHz o interrumpidos por reset si este pulso aparece.
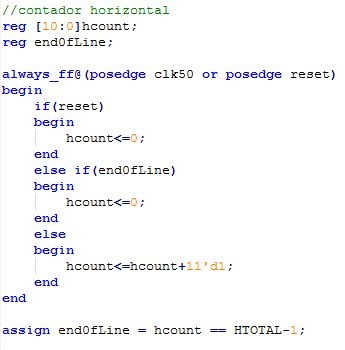
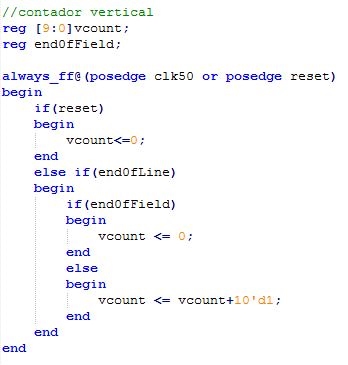
Las señales end0fLine y end0field indican como su nombre lo indica el fin de una línea barrida o de un frame.
Se añaden otras señales que tienen la mismas funciones que las descritas en el módulo mi_vga de la primera parte
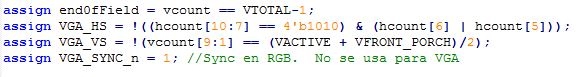
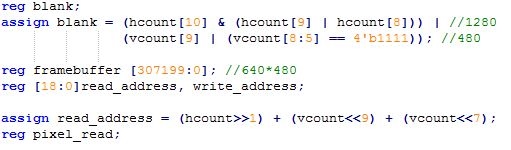
En el bloque always a continuación, se indica cuándo el barrido corresponde al área visible.

Al final se asigna el bit menos significativo del conteo al reloj, lo que hace que la señal presente un cambio de estado que resulta en un reloj de la mitad de la frecuencia del conteo, es decir de 25MHz.
El dato que se lee en el registro framebuffer en la posición read_adress, se asigna a las salidas R, G y B, para conectar al siguiente módulo.

- Hallway: Generador de línea
En este módulo se describe una máquina de estados que lleva la información de la línea a el módulo bresenham para ejecutar el algoritmo.
Se declara la variable que determinará el estado en el que se encuentra la máquina.

Crea el bloque always donde se describirá la máquina de estados, también el nivel de las señales de salida si se activa el reset. Define a S_TOP como el estado predeterminado.

Se define el case con el primer estado, en el cual la salida start se activa para una señal de done en alto, y se asigna el comportamiento de x0.

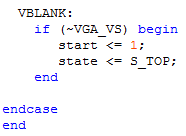
Los siguientes estados se definen a continuación:



Define que cuando VGA_VS está en bajo se está fuera de la zona visible de la pantalla.
Resultados
Ya con los módulos necesarios, regresamos al chip principal para hacer las instanciaciones y probar el resultado final.
Se necesitan algunos cables para hacer las conexiones entre los módulos, y asignar a los pines de salida.
En el módulo bresenham se conectan las entradas de start, done, las coordenadas de entrada para la línea que se va a dibujar, y las señales x y y de salida al framebuffer.
Para el framebuffer se conectan los datos de color que se asignan a la salida para su conexión al cable VGA.
Lo mismo para el módulo hallway.
Referencias
- http://www.cs.columbia.edu/~sedwards/classes/2016/4840-spring/
- https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm
- https://sites.google.com/site/ece10243upb2016/2-simulacion-y-fsm
- Pong P. Chu, "Embedded SoPC Desing with Nios II Processor and Verilog Examples"
- Stephen A. Edwards, "Drawing Lines with SystemVerilog"